跳转至

算法设计与分析

第一部分:算法设计和分析的数学和定理基础

算法设计的两个例子

调度问题

image-20220709155025889

贪心法的解:按照加工时间从小到达安排,即3,5,8,10,15

image-20220709155422811

贪心算法的反例:

image-20220709155612083

按照贪心算法:单位重量价值最大的优先,按照 价值/重量 从大到小排序

image-20220709155811404

然而存在更优的解:

image-20220709155837492

==算法设计:==

image-20220709155930398

投资问题

image-20220709160719604

对问题进行建模:

image-20220709160804527

蛮力算法(枚举):将每一种可能的分配方案计算出结果,选择最优的解

蛮力算法的效率:

​ 数学的求解过程:(可只关注结论)

image-20220709161356269

image-20220709161411655

结果的推导过程参考:stirling公式

image-20220710120504269

结论:蛮力算法的效率为指数函数,效率极低.==因此有些问题容易找到好的算法,有些问题需要设计更好的算法==

image-20220709161726061

问题计算复杂度的界定:以排序问题为例

image-20220709161819814

以上算法的具体过程见数据结构

问题计算复杂度的分析:同一个问题的不同种算法同时考虑分析

​ 哪个排序算法的效率最高?

​ 排序问题的难度?

货郎问题与计算复杂性理论

货郎问题:

image-20220709164314260

问题的建模:

image-20220709164341821

0-1背包问题:

image-20220709164422674

问题的建模:

image-20220709164457229

双机调度问题:

image-20220709164535856

问题的分析:

image-20220709164610868

==以上问题都没有找到有效的算法可以解决,被称为NP-Hard问题==

NP-Hard问题:

​ 存在大量的这类问题

​ 至今没有找到有效算法:现有算法的运行时间是输入的指数或更高级别

​ 至今没有人能证明不存在这类问题的多项式时间的算法

​ 从多项式时间的算法角度来看,这类问题等价,这类问题的难度处于可有效计算的边界

image-20220709165151580

课程内容:

image-20220709165219209

算法及其时间复杂度

问题及实例的概念

image-20220709202248984

算法的概念

image-20220709202428286

基本运算与输入规模

image-20220709204214987

​ 输入规模:

image-20220709204307230

​ 基本运算:

image-20220709204339740

算法的两种时间复杂度

image-20220709204026428

平均时间复杂度的计算

image-20220709204103789

算法的伪码表示

算法的伪码描述

image-20220710095747150

求最大公约数:欧几里得算法

image-20220710095913030

image-20220710110505269

小结

image-20220710110534797

函数渐进的界

大O符号:可以接触到的上界,fn阶数不高于gn

image-20220710111806732

image-20220710112032777

大Ω符号:可以接触到的下界,fn阶数不低于gn

image-20220710112118007

image-20220710112144487

小o符号:接触不到的上界,fn阶数低于gn

image-20220710112232578

image-20220710112521035

小Ω符号:接触不到的下界,fn阶数高于gn

image-20220710112605122

image-20220710112625696

Θ符号:既是可接触的上界又是可接触的下界,fn和gn阶数相同

image-20220710112725836

image-20220710112832238

时间复杂度:O(n^1/2^) //可接触的上界

有关函数渐进界的定理(计算时间复杂度时使用)

image-20220710113728582

用于判断fn和gn的阶数高低

推论:

image-20220710113831530

image-20220710113850974

用于判断时间复杂度为对数,幂函数,指数函数时的关系大小

image-20220710114013719

用于判断各函数的阶数大小关系

image-20220710114518208

用于判断一个算法中不同基本运算次数在时间复杂度上取哪个(算法的时间复杂度是各步操作之和,在常数步的情况下取最高阶的函数即可)

几类重要函数

基本函数类

image-20220710115833216

==指数>多项式>对数多项式==,每一级都相对于上一级爆炸增长

指数级的算法是不可运算的!

对数函数

​ 简写说明:

image-20220710120000135

​ 性质:

image-20220710120029211

​ 1.在考虑算法的复杂度时不需要考虑对数底的大小

​ 2.对数要小于幂函数

​ 3.此情况下对数指数函数和幂函数相等

指数函数与阶乘

image-20220710120235723

阶乘要小于n^n^,要大于2^n^,阶乘的对数和nlogn同阶

取整函数

image-20220711084842764

性质:

image-20220711084935024

按照阶排序的实例

image-20220711085232515

从左到右阶数依次变小,从上往下量级依次变小

序列求和的方法(求迭代过程的算法的时间复杂度)

求和公式

image-20220711091046450

一个例子:

image-20220711091205353

应用:二分检索法的平均时间复杂度

image-20220711092043473

image-20220711091332542

image-20220711091455914

估计和式上界的放大法

image-20220711092520799

一个例子:

image-20220711092613094

估计和式渐进的界:

image-20220711092727662

image-20220711092808059

结论:调和级数和logn同阶

递推方程与算法分析(递归的算法的时间复杂度求解)

递推方程的定义

image-20220711094204606

几个例子

fibonacci数列:

image-20220711094250514

最下面的红框即为递推方程的解

汉诺塔问题:

image-20220711094417387

image-20220711094448777

利用迭代求递推公式的解

即时间复杂度为指数级!

==这是一个难解问题,不存在多项式时间的算法==

插入排序

image-20220711094643986

W(n-1)为上一个元素插入排序的时间复杂度,n-1为这一个元素最坏情况下需要比较的次数

利用迭代求递推公式的解

迭代法求解递推方程

直接迭代

image-20220711102559786

以汉诺塔为例做迭代求递推公式的解:

image-20220711102905228

换元迭代

image-20220711103014457

以二分归并排序为例做换元迭代:

image-20220711103119385

W(n/2)为后面两次递归的排序的时间复杂度,n-1为这次排序需要对比的次数

image-20220711103248099

可以用数学归纳法验证正确性

image-20220711103525939

差消法化简高阶递推方程(以快速排序的时间复杂度分析为例)

快速排序时间复杂度分析:

image-20220711104832931

image-20220711104906742

image-20220711104926597

平均工作量=总工作量/输入情况个数n

image-20220711104952644

差消化简:利用两个方程相减,将右边的项尽可能消去,以达到降阶目的

image-20220711105208956

下面两式相减,可消去∑处的大部分项

image-20220711105534480

image-20220711105556224

递归树(是迭代的模型)

递归树的概念

image-20220711111010181

迭代在递归中的表示:

image-20220711111048087

递归树的生成规则:

image-20220711111249791

==递归树往往使用在需要迭代的项数大于1的情况==

实例一:以二分归并排序的时间复杂度分析为例做递归树的应用

image-20220711111322100

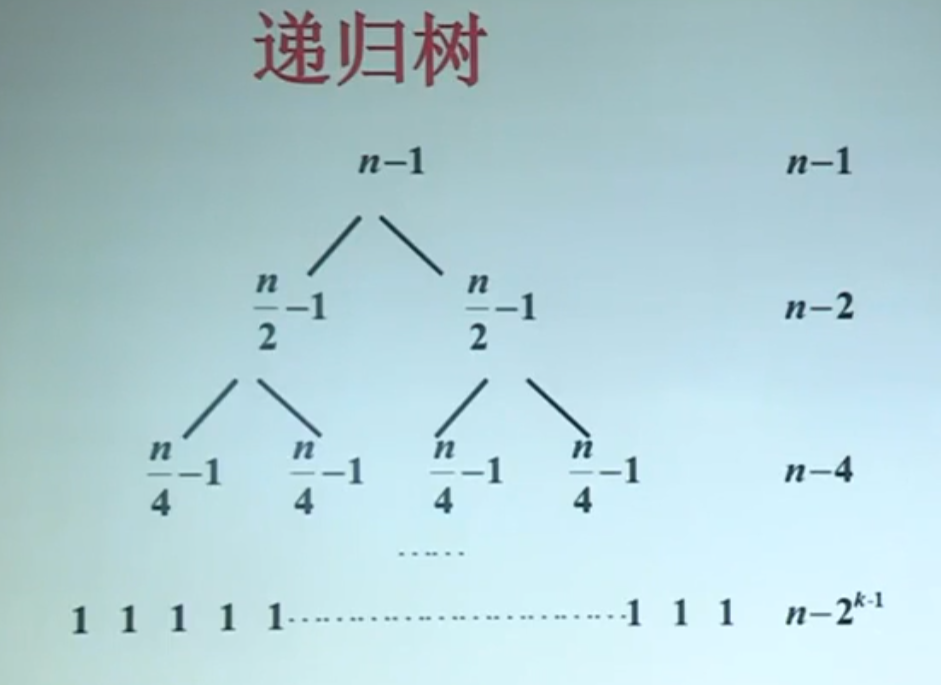
image-20220711111343390

写出递归树前几层后,==分析每一层的总和,根据每一层的规律推导出总的时间复杂度==

image-20220711111512954

实例二

image-20220711111713710

==注意==:这棵迭代数左边递减速度大于右边,所以树右边的层数会大于左边,因此最后一层的总和不超过n,即O(n)

image-20220711112709144

这里的求和只看最右边这一路:每一次迭代乘以2/3,总共迭代k次,即最后一层的表达式为(2/3)^k^n,等于最后的初值为1,从而求出k

最后得到:

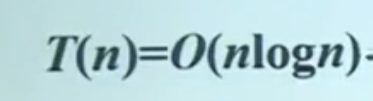
image-20220711113238709

logn为层数k,n为每层的总和

主定理及其应用(用于求解递推方程的解,得到时间复杂度)

主定理的应用背景

image-20220712091820813

主定理的概念:

image-20220712091857618

主定理的应用:

image-20220712100141461

image-20220712094747470

image-20220712095006493

image-20220712100028681

image-20220712100056882

不可以使用的例子:

image-20220712100206508

使用递归树求解:

image-20220712100241674

image-20220712100300888

第二部分:分支算法的设计思想与分析方法

分治策略的设计思想

分治策略的基本思想

image-20220712102126730

几个例子

二分检索:

image-20220712102217361

image-20220712102302285

二分归并排序:

image-20220712102325015

image-20220712102344406

image-20220712102416054

汉诺塔问题:

image-20220712102445095

image-20220712102511234

分治算法的一般描述和分析方法

分治算法的一般描述

image-20220712103313699

1.当P问题足够小到量为c时,可以直接求解

分治算法的设计要点

image-20220712103513150

分治算法的时间复杂度分析

image-20220712103546253

fn为在划分时需要消耗的工作量以及综合问题时的工作量

Wc为划分到最小时的工作量

==分治算法两类常见递推方程及其时间复杂度分析==

image-20220712103852438

image-20220712103909799

==方程2常用以下结论直接得出时间复杂度:(由主定理推导得到)==

image-20220712104016150

典型分治策略算法1:芯片测试

image-20220712113228307

首先考虑两个芯片之间相互测试可能存在的情况:

image-20220712151826536

image-20220712151852483

接下来分析用其他所有芯片判断一颗芯片好坏的可能性

​ 奇数情况:

image-20220712152052168

​ 偶数情况:

image-20220712152112535

最后考虑整个问题的算法:

一 蛮力算法

image-20220712152223013

最坏情况时间复杂度为On^2^量级

==二 分治算法==

image-20220712152333088

==注意==:该算法在递归调用一次后,仍然满足好芯片比坏芯片多一颗的条件,接下来证明这个结论:

image-20220712152621000

n为偶数时显然满足

image-20220712152659240

n为奇数时,若按照原方案,则存在轮空芯片,导致算法出错;

因此需要单独对轮空芯片与其他芯片比较,判断其好或坏(见前文如何判断一颗芯片的好坏)

分治算法的伪码表示:

image-20220712153059656

分治算法的时间复杂度分析:

image-20220712153208836

结论:分治算法要优于蛮力算法

典型分治策略算法2:快速排序

基本思想:

image-20220712155451037

伪码表示:

image-20220712155523650

image-20220712155606167

实例:

image-20220712155636813

==注意==:与之前学习的稍有区别,体现在之前有一个辅助空间储存中间值,从而使得发现一个需要交换的数直接进行交换;结束条件为前指针位置大于后指针位置时

​ 此处为先从后向前找再从前向后找,都找到需要交换的值时再进行调换;结束条件为找到需要交换的第一组前指针大于后指针的情况

时间复杂度分析:

image-20220712160225045

最坏情况:中间值为数组中最大的数/最小的数

当每次划分比例保持不变时,时间复杂度仍为O(nlogn)

image-20220712160403843

推导过程:递归树(类似于递归树中的示例二)

image-20220712160510691

平均时间复杂度分析:

image-20220712160559164

image-20220712160620307

==注意==:红框中的式子使用差消法求得递推方程的解

结论:快速排序的的时间复杂度:

​ 最坏:O(n^2^) 平均:O(nlogn)

典型分治策略算法3:幂乘算法及其应用

image-20220713093650679

使用分治算法划分:

image-20220713093821678

分治算法的时间复杂度分析:

image-20220713093944149

幂乘算法的应用:fibonacci数列的矩阵运算

传统算法:

image-20220713094418466

fibonacci数列的矩阵相关性质:

image-20220713094501080

利用幂乘计算fiboncci数列的算法以及时间复杂度分析:

image-20220713094732668

改进分治算法的途径1:减少子问题数

image-20220713101002349

实例一:整数位乘问题

image-20220713101103006

此处的四条红线分别是需要计算的四个子问题

发现分治算法并没有降低时间复杂度

减少子问题的个数从而降低分治算法的时间复杂度:

image-20220713101158705

这次子问题被缩小到了三个,有效的降低了时间复杂度

实例二:矩阵相乘问题

image-20220713101513278

采用简单分治算法:

image-20220713101544462

此处有八个子问题需要计算,与传统算法的时间复杂度相同

通过Strassen矩阵乘法,将子问题缩小到7个:

image-20220713101841140

image-20220713102115425

矩阵乘法的应用:

image-20220713102146775

改进分治算法的途径2:增加预处理,减少fn

以平面点对问题为例:

image-20220713110158288

算法伪码:

image-20220713111118455

跨边界情况的处理:

image-20220713111153210

==注意==:δ为左半边和右半边最小长度中的最小值,而每个方格中最长的长度(对角线)为5δ/6,因此每个方格最多有一个点

​ (因为如果一个方格里有两个点说明他们的距离小于δ,δ就不再是左半边和右半边最小长度中的最小值)

算法时间分析:

image-20220713112000377

增加预处理,减少排序的时间:

image-20220713112101685

拆分的时间复杂度为On

拆分过程的实例:

image-20220713112504397

对XY都直接排序

X:直接从中间拆分 Y:将左半边的移到右侧,右半边的移到左侧

改进算法的时间复杂度分析:

image-20220713112656704

时间减少了一个logn

典型分治策略算法4:选择问题

image-20220713115240415

选最大与最小

只选最大/最小:

image-20220713115309326

同时选择最大和最小:

普通算法(顺序比较):

image-20220713115403875

分组算法:先两两分组,将大的分为一组小的分为一组,在大的组中找最大值,小的组中找最小值

image-20220713115532843

最坏时间复杂度分析:

image-20220713115604772

分治算法:将数组从中间划分,递归的求左右两个子数组的最小值和最大值,最后比较最外面一层的左右最大值和最小值

image-20220713115736161

最坏时间复杂度分析:

image-20220713115805269

结论:

image-20220713115829119

只选最大/最小:顺序比较已经是最好的算法了

同时选最大和最小:顺序比较不够优秀,分组和分治是最好的算法

选第二大

image-20220714104402584

提高效率的算法:锦标赛算法

image-20220714104440753

==重点:以时间换空间==

image-20220714104519516

image-20220714104539266

实例:

image-20220714112142455

分析时间复杂度:

image-20220714112225254

image-20220714112354293

说明最大值所淘汰的数总共有logn上取整那么多,从而得到第二阶段的时间复杂度

image-20220714112649237

一般选择问题的算法设计

image-20220714114815994

应用该问题的实例:管道位置问题

image-20220714114854880

实例分析:

image-20220714120055662

结论:最优解为y坐标的中位数之间修管道

简单算法:

image-20220714120206062

分治算法:

image-20220714120434033

为了保证效率,需要设计找到合适的m^*^的算法:

​ 将整个数组划分成n/5下取整个组,每组从大到小排列,从而通过选择算法确定中位数组中的中位数作为m^*^

image-20220714120536784

​ A,D两个区中数字的大小和m^*^的大小关系无法确定,因此需要一一对比,将大的数划分进B,小的数划分进C

实例:

image-20220714120929338

image-20220714120949570

算法伪码:

image-20220714121138073

一般选择问题的算法分析

算法的时间消耗主要在三次递归调用上消耗

子问题的规模分析:

image-20220714152827310

因此算法的时间复杂度为:

image-20220714152912747

递推方程为:

image-20220714152953347

通过递归树求解得:

image-20220714153025935

==思考==:之前讨论的都是五个元素一组,若修改每组元素个数,如3/7个,算法时间复杂度会改变吗?

image-20220714153203132

以3分组时为例分析时间复杂度:

image-20220714153300235

image-20220714153332678

当3分组时,递归树的每一行不构成公比小于1的等比数列,因此复杂度增加

结论:当3分组时时间复杂度增加,为O(nlogn),而5,7分组时为O(n)

经典分治策略算法应用1:卷积

卷积及其应用

向量计算

image-20220714154654481

卷积:下标之和为k的相同的每组数相乘再相加,得到c~k~的值

卷积计算用矩阵表示:

image-20220714154735574

实例:

image-20220714154854320

卷积与多项式乘法的关系:卷积的每个分量的值和多项式的每一项对应

卷积的应用:信号的平滑处理

image-20220714155033178

image-20220714155054178

蓝框为信号向量a 红框为权向量b 权向量的长度=2*步长+1

==注意==:信号向量两头不能完全取到所有权向量的值会产生误差

实例:

image-20220714155345202

使用矩阵表示:

image-20220714155411395

卷积计算

蛮力算法

image-20220714165605780

时间复杂度为O(n^2^)

快速傅里叶变换FFT算法

​ 基本原理:

image-20220714165827870

​ 问题:如何选择x~0~到x~2n-1~,使得多项式求值算法高效

​ 高斯滤波的权值函数:

image-20220714170133411

​ 2n个数(x)的选择:1的2n次根

image-20220714170253677

​ 实例:

image-20220714170331254

快速傅里叶变换FFT算法思路:

image-20220714170405662

最后利用以下等式关系:

image-20220714170657681

算法的关键:

image-20220714170852563

接下来研究,对多项式快速求值的算法

法1:蛮力算法

image-20220714172414511

法二:改进的求值算法

image-20220714172520734

法三:分治算法(奇系数和偶系数多项式)

实例:

image-20220714172655142

一般公式:

image-20220714172753502

image-20220714173111432

从而分解出两个子问题递归调用的工作

分治算法的时间复杂度分析:

image-20220714173250360

FFT算法伪代码

image-20220714173353501

算法分析:

image-20220714173415553

经典分治策略算法应用2:平面点集的凸包

image-20220718093039268

分支的算法:

image-20220718093658201

image-20220718093724430

算法时间复杂度分析:

image-20220718093821471

分治算法小结

image-20220718094459771

image-20220718094515507

image-20220718094554492

第三部分:动态规划

动态规划算法的例子

image-20220718095702239

image-20220718095933136

实例:

image-20220718095956979

算法设计:

image-20220718100031032

动态规划求解:

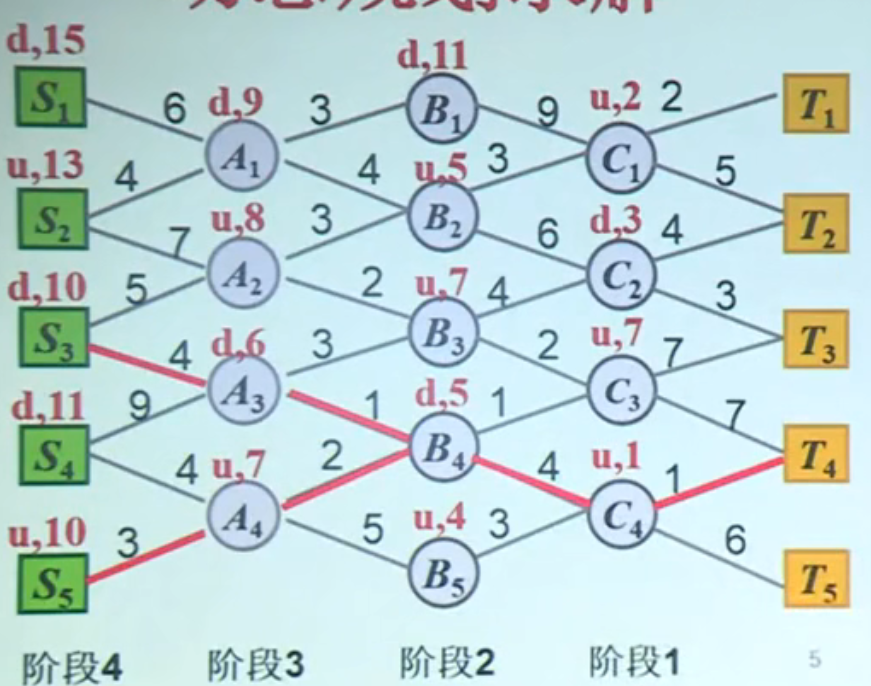
image-20220718100109732

从终点往起点的顺序考虑,每次标记最短路径以及是往上走还是往下走

动态规划算法特点分析:

image-20220718100523916

image-20220718100549274

==关键==:每一步决策与上一步决策的结果存在依赖关系

image-20220718100807336

一个反例:

image-20220718101329412

解释: 模10的最小路径:路径长度%10以后结果最小

无法使用动态规划的原因:不满足优化原则,如第一个子问题(最后一个点到终点的路径选择)的正确结果并不是该子问题的最优解

小结:

image-20220718101632033

动态规划算法设计

image-20220718103008688

矩阵链相乘问题:

image-20220718103033328

分析矩阵相乘基本运算次数:

image-20220718103235856

实例:

image-20220718103344556

蛮力算法:时间复杂度极高

动态规划算法设计:

image-20220718103438844

递推方程:

image-20220718103528185

小结:

image-20220718103803738

动态规划算法的递归实现

image-20220718105643358

通过证明得到:动态规划的递归实现的算法时间复杂度仍旧为很高,达到2^n^

原因:

image-20220718105834507

相同颜色的为相同的子问题

image-20220718105904306

==子问题有大量的重复运算!==

image-20220718105947291

动态规划算法的迭代实现

image-20220718112142027

image-20220718112157530

伪码:

image-20220718112300278

时间复杂度:

image-20220718112536111

实例:

image-20220718112606803

image-20220718112641498

image-20220718112905298

两种实现的比较:

image-20220718115558244

动态规划算法的要素:

image-20220718115628321

投资问题

image-20220719203220953

实例:

image-20220719203242214

子问题的界定和计算顺序:

image-20220719203734069

注意:不同于矩阵链相乘问题,投资问题的两个参数类型不同

先考虑前k个问题的最大值,每个问题都要考虑x的所有可能

优化函数的递推方程:

image-20220719203954877

计算实例:

image-20220719204155137

image-20220719204213866

image-20220719204454026

时间复杂度分析:

image-20220719204832210

image-20220719204855502

小结:

image-20220719204920761

背包问题

image-20220719212211439

问题建模

image-20220719213734752

image-20220719213755078

image-20220719213821938

image-20220719213840154

实例:

image-20220719213859656

image-20220719214015385

image-20220719214036581

image-20220719215738019

推广:

image-20220719215816846

小结:

image-20220719215840531