跳转至

计算机图形学GAMES101几何

几何归类

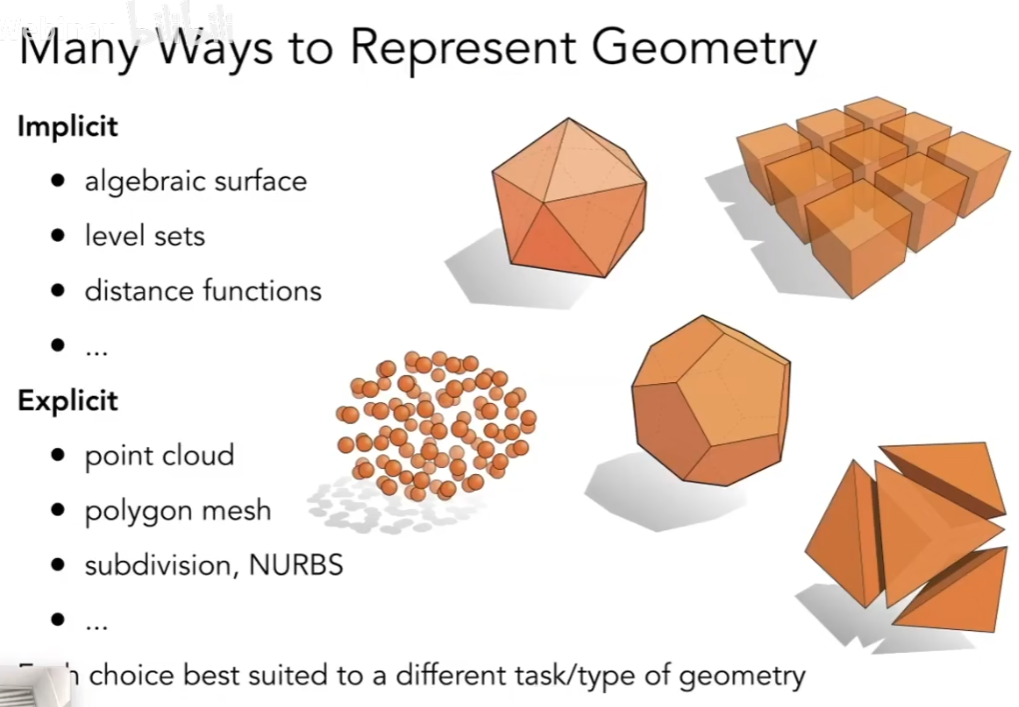
image-20220820162532964

  • 几何分为:隐式和显示

隐式几何

image-20220820162907487

  • 隐式几何:点通过关系式来描述,而不是一个个明确的点

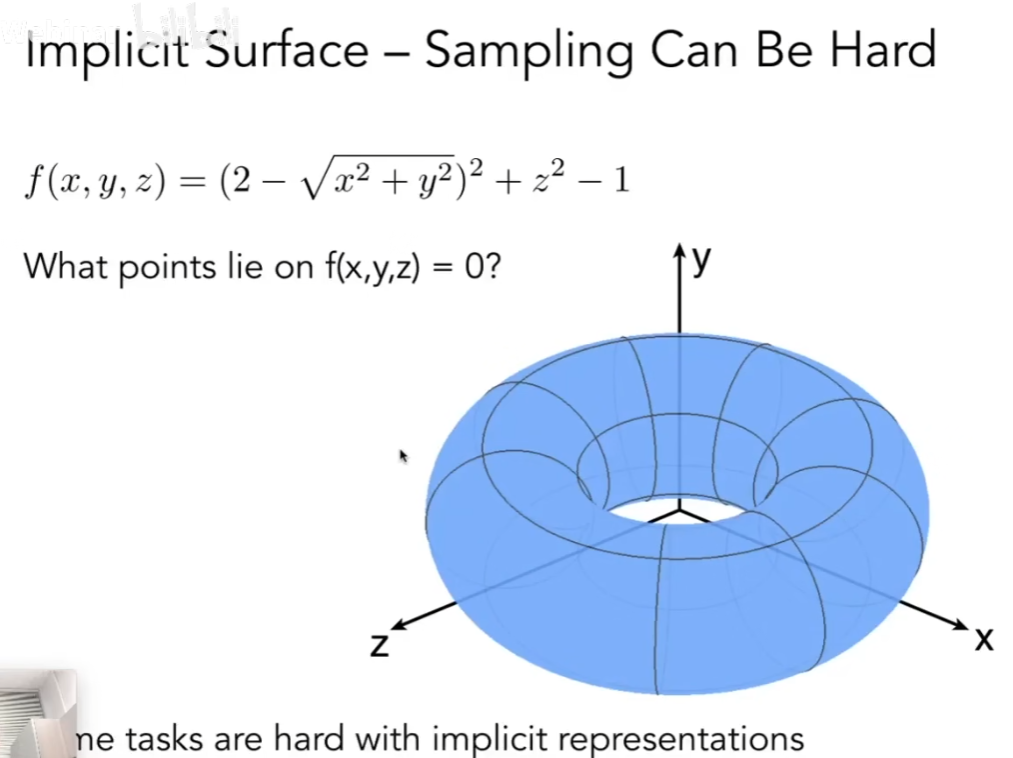
image-20220820174025188

  • 隐式表示的缺点:难以直接判断形状

image-20220820174144884

  • 隐式表示的优点:便于判断点与几何之间的位置关系,代入函数:
  • =0,在表面
  • <0,在物体内
  • ＞0,在物体外

显示几何

image-20220820175036659

  • 显示几何:直接给出点 或者 通过参数映射表示

image-20220820175157488

  • 如上式,就是一个参数uv对应到xyz的表示
  • 显示表示的优点:便于直接观察得到几何形状

image-20220820175507027

  • 显示表示的缺点:难以判断点与几何的位置关系

==根据需要选择表示方法==

隐式的其他表示方法

image-20220820175754300

  • 数学代数表示,不直观

CSG

image-20220820175935803

  • 通过基本几何的布尔运算得到复杂几何

距离函数

image-20220820180226635

  • 距离函数:空间中的点到几何体最短的距离
  • 距离为正,在几何体外;距离为负,在几何体内
  • 两个几何的距离函数进行融合后,再恢复成物体,得到融合后的物体

image-20220820181211872

  • 上例:阴影代表物体对屏幕的遮挡,求出输入A运动成输入B的中间状态
  • 如果直接融合(blend,即相加求平均值),得到的结果并不是中间状态,而是黑灰白三块
  • 正确做法:求出两种输入的边界函数,再进行blend(即找到距离函数=0的位置),最后恢复成最终结果,得到的就是中间值

image-20220820200607429

  • 水平集:距离函数不方便用解析的形式去表示,因此使用水平集(如图)去表示
  • 水平集也可以在三维上
  • 水平集的应用:水滴之间的融合效果

特殊的隐式几何:分形

image-20220820201224030

  • 分形:自相似,自己的一部分和整体很像,类似于计算机中的递归

隐式优缺点

image-20220820202133676

  • 隐式缺点
  • 不便于直接判断形状

  • 复杂的几何难以表述

  • 隐式优点

  • 但是式子便于储存
  • 便于查询与点之间的位置关系
  • 便于求光线和表面的交
  • 适合描述拓扑结构
  • 几何弧度描述优秀

显示几何的其他表示方法

点云

image-20220821175114061

  • 不考虑面,而是密集的点
  • 可以表示任何几何
  • 扫描出的原始数据一般为点云
  • 点云->多边形面
  • 不常用

多边形面

image-20220821175313697

  • 将几何拆分成小的三角形和四边形
  • 广泛应用

image-20220821175331749

  • .obj文件
  • 包含点的坐标,法线,纹理坐标,以及他们之间的连接关系(哪三个点形成一个三角形)
  • v点 vt纹理坐标 vn法线

曲线和曲面

贝塞尔曲线

image-20220821181018304

  • 使用一系列控制点定义曲线
  • 起始点必须为p~0~和终点必须为p~3~
  • p~0~处切线必须沿p~0~p~1~方向,p~3~处切线必须沿p~2~p~3~方向
  • 不一定要经过中间的控制点
  • 属于显示几何表示

de Casteljau算法(如何画出贝塞尔曲线)

image-20220821181717300

在二次贝塞尔曲线情况下

  • 通过画出不同位置的点,从而得到曲线
  • 假设起始点时间为0,终点时间为1,所画的点位于t
  • 找到b~0~b~1~和b~1~b~2~线段上t位置的点
  • 将不同线段上的两个t位置的点连线,找到连线上t位置的点,该点为贝塞尔曲线在时间t时所在的点

image-20220821181831941

  • 找遍所有0到1时间的点就是贝塞尔曲线
  • 类似递归

image-20220821182024705

  • 三次贝塞尔曲线同理

贝塞尔曲线的代数表示

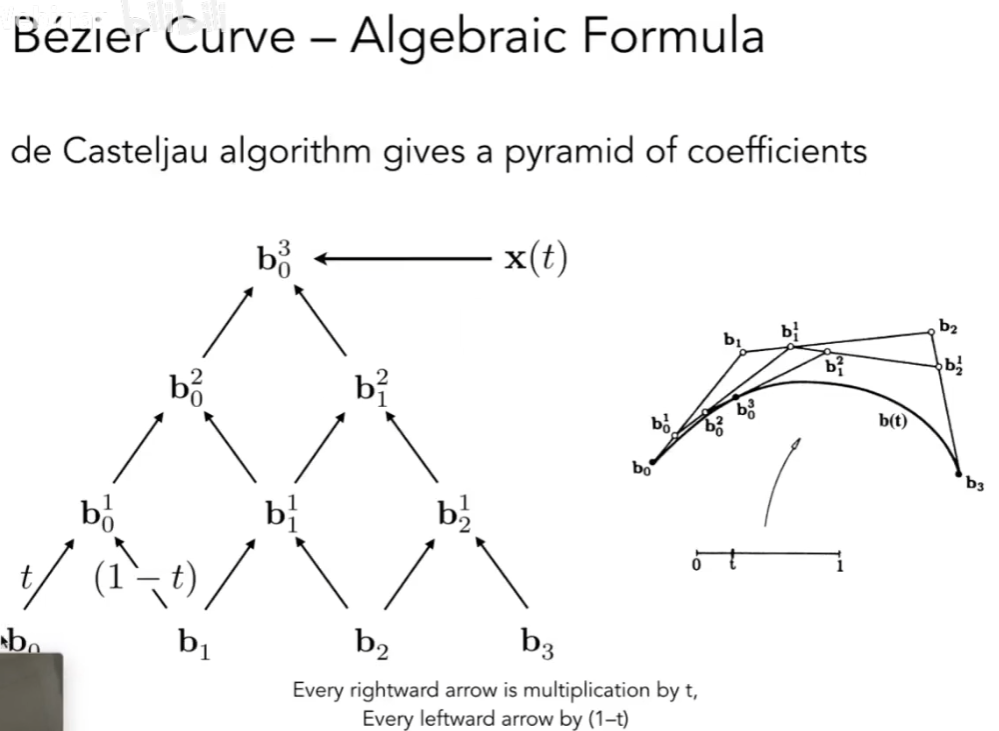
image-20220821182254090

  • 不停的线性插值得到

image-20220821182929005

在二次贝塞尔曲线中:

  • 结果的点是b~0~,b~1~,b~2~的组合,且与t有关

  • 类似于下式的展开 $$ [(1-t)+t]^2 $$

  • 同理,三次贝塞尔曲线中为 $$ [(1-t)+t]^3 $$

image-20220821215204837

  • 贝塞尔曲线可以用控制点的线性组合进行表示

  • ∑后第一项为控制点

  • ∑后第二项为伯恩斯坦多项式,即 $$ [(1-t)+t]^n $$

image-20220821220100870

  • 控制点也可以是三维的

image-20220821221104627

  • 由于伯恩斯坦多项式实际上是1的n次方,因此t为0到1的任意值时,多项式之和一定为1

贝塞尔曲线的性质

image-20220823155217959

  • 起始点一定为b~0~,终点一定为b~3~
  • b~0~处切线必须沿b~0~b~1~方向,b~3~处切线必须沿b~2~b~3~方向
  • 对贝塞尔曲线直接仿射变换的结果和对控制点进行仿射变换后画出的贝塞尔曲线是一样的(仅限于仿射变换,如投影不可以)
  • 凸包性质:贝塞尔曲线一定在控制点形成的凸包内

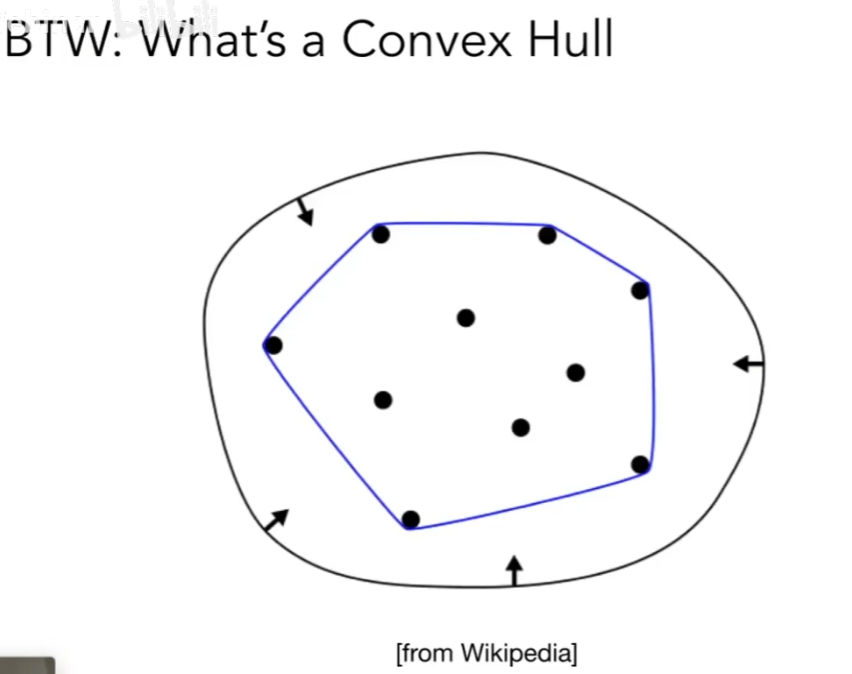
image-20220823155515521

  • 凸包:能够包围给定几何形体的最小凸多边形

逐段的贝塞尔曲线

image-20220823155811350

  • 控制点太多时,曲线不好控制

image-20220823155829308

image-20220823160939260

  • 逐段贝塞尔曲线:通常使用四个控制点(三次贝塞尔曲线)定义一段曲线
  • 将控制点变成拉杆式的设计
  • 逐段贝塞尔曲线的控制点如上图
  • 让两端贝塞尔曲线连续的必要条件:切线的方向相同且距离中间点的大小相同

image-20220823161420465

  • C^0^连续:上一段的最后一个控制点和下一段的第一个控制点相同,也就是几何上的连续(连起来即可)

image-20220823161356457

  • C^1^连续:上一段的最后一个控制点上的切线和下一段的第一个控制点上的切线方向大小都相同,也就是光滑(一阶导数连续)

其他曲线

样条

image-20220823161640135

  • 连续的曲线
  • 由控制点控制
  • 任意点满足特定连续性
  • 可控的曲线

B样条

image-20220823162229121

  • 基函数样条
  • 局部性:修改一个控制点只会影响局部的形状

曲面

贝塞尔曲面

  • 贝塞尔曲面由贝塞尔曲线形成
  • 首先在平面上4*4的控制点image-20220823163122317
  • 接着得到四个贝塞尔曲线image-20220823163141600
  • 这四个贝塞尔曲线上的点作为控制点,得到贝塞尔曲面image-20220823163205293image-20220823163239157

image-20220823164334338

  • 由于四个曲线需要一个时间t,曲线上的四个点连成后还需要一个时间t,所以需要二维的uv两个变量控制

网格操作

image-20220919190908663

  • 网格细分:用更多三角形得到更加光滑的结果
  • 网格简化:用更少三角形简化模型,会丢失模型质量
  • 网格正规化:都变成近似正三角形,会丢失模型的质量

曲面细分

Loop 细分

(Loop为人名,与循环无关)

前提条件:物体必须由三角形网格形成

image-20220919192253834

  • 利用三角形三边的中点,增加三角形的数量,划分成4个三角形
  • 更新顶点位置,新的顶点和老的顶点分开调整

新顶点的位置更新:

image-20220919200915082

  • 对于两个三角形公用边上新的顶点:
  • 公用边的端点为AB,其余两个三角形端点为CD
  • 根据上述公式加权平均得到新的点的位置

旧顶点的位置更新:

image-20220919201331863

  • n为旧顶点的度(有几个边经过)
  • u为与n有关的数
  • 根据上述公式加权平均得到新的位置
  • 该加权公式的特点:顶点周围的点越多(度越大),自身原本的位置权重就越小,周围点的位置的权重就越大

Catmull-Clark细分

任何网格体都能细分

image-20220919202652190

基本概念:

  • 非四边形面
  • 奇异点:顶点的度!=4的顶点

image-20220919202749138

一次细分操作:

  • 将每个边的中点作为新的顶点
  • 将每个面的中心点作为新的顶点
  • 连接每个面边上的新顶点和中点得到结果

一次细分的特点:

  • 细分前有多少个非四边形面,一次细分后就会增加多少个奇异点
  • 在之后的细分中,奇异点的数量不会再增加

image-20220919203239145

  • 新的平面中心,新的边上的中点,老的点,都会根据特定公式在一次细分中更新位置

曲面简化

边坍缩

image-20220919204511139

如何确定坍缩后新的顶点位置?

image-20220919204805690

  • 二次误差度量:保证新的顶点到坍缩前周边的面的距离的平方和最小

如何确定选择哪条边进行坍缩?

image-20220919205641179

  • 计算坍缩每个边所对应的二次误差并记录
  • 由于坍缩一个边会影响其他边的二次误差,因此需要使用优先队列(堆)来动态更新其他边的二次误差
  • 找到二次误差最小的边
  • 二次误差度量法通过局部最优解达到整体最优:贪心算法